Solidworks开坑:绘制摇杆-已知球缺求原球体
前言
此项目来自于工作需求,起因是我司维护的某款机器一个零件缺货,该零件是用于将摇杆电位器连到机器外操作摇杆的一系列零件中的一个结构件。因该机器是一款儿童玩具,损坏几率不低,没有本零件将无法为其修复。为此计划使用3D打印机制作该零件,且因公司不提供该零件的3D模型文件,为解决此问题,建立本项目。
准备
因之前没有接触过3D建模领域,所以该项目查找了大量网络资料。通过查找资料得知,这种工件类设计使用Solidworks(后称SW)比较合适。于是通过查找资料,采用边学习边做的方式尝试对该零件进行建模。
零件形状如图所示;
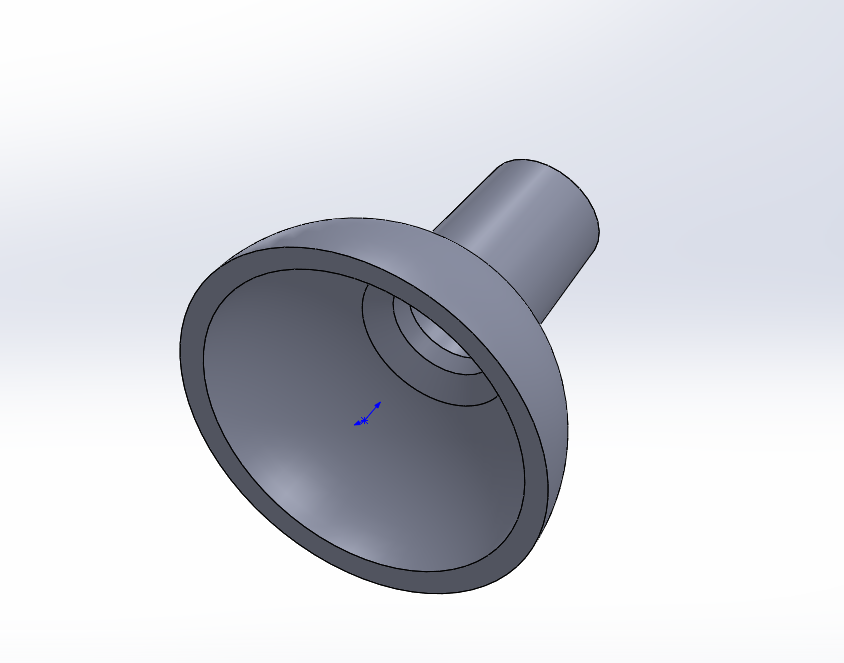
考虑零件形状,组成结构类似于一个半球上加一个圆柱,内部是空的,该零件是左右对称的解构。通过搜索引擎得知,SW可以通过草图旋转产生3D模型,于是我们就需要设计一个可以用于旋转产生的草图。
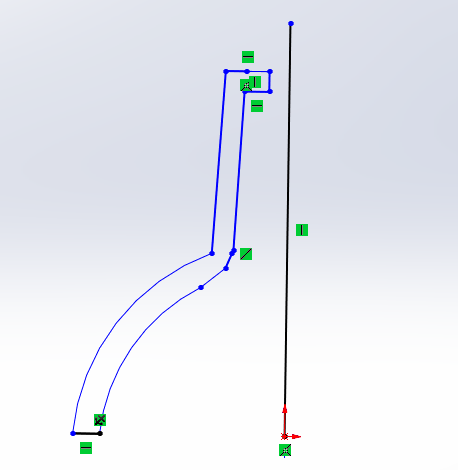
接下来事情是要确定下面那个类似半球的结构,其底面直径可以测出,但是观察发现,这个并非一个半球,这个球缺比它所属的球的半球小,这样我们就要先算一下这个球缺所属球体的数据。
求解过程
我先画了一个截面图,能够测量出的数据有a = 14.5mm,b = 15.75mm;设r为原始球体的半径,则a+y = r。
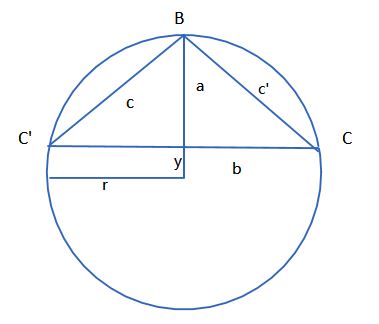
根据三角行外接圆半径公式
$R = \frac{abc}{4s}$
这个公式中的字母与我图中画的无关,其中R是圆的半径,abc分别为三角形三边的长,S为三角形的面积。如图可见,三角形BCC'是这个圆的内接三角形。
公式套到我的图中就是:$r = \frac{2bcc^′}{4 \frac{2ba}{2}}$ ;下图
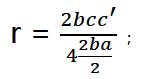
代入勾股定理得;
r = (2b(√(a^2+b^2 ))^2)/(4 2ab/2),下图
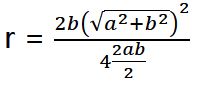
化简后得到:
r = (a^2+b^2)/2a,下图
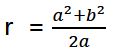
将数值代入公式;
r = (14⋅5^2+〖15.75〗^2)/(2×14.5)= 15.8(约值),下图
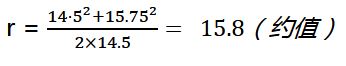
至此,我算出了那个球的半径r约为15.8mm
那么,y值约为15.8-14.5 = 1.3mm